A tale of heat and moisture: chasing the advective fluxes

Undeniably, eddy covariance has come a long way (i.e. sensor development and data processing) thanks to the immense collaborative effort across different communities (Foken et al., 2012). For high-frequency losses, we can use spectral analysis and transfer function to adjust fluxes (Moore, 1986; Massman, 2000). For validating remote sensing models, we can constrain fluxes within a representative area using footprint analysis (Kljun et al., 2015). But, for over 30 years, the energy balance closure problem continues to haunt us (Foken, 2008). To some, a lack of closure is ominous, and for convenience forced closure method (Twine et al., 2000) is often used.

Routinely, we have treated land segments as silos and gravitated our perspectives towards fluxes that are directed upward and downward. If you have ever had a leaky sink, one way to fix it would be to put a bucket underneath. But wouldn’t it make more sense to find and fix the core problem that is causing the leak? Nature perhaps is similar to the leaky sink, but on a far more complex scale, and the core problems are often from many different sources and sinks. So, what cause(s) our control volume to leak and unable to conserve energy? In essence, fluxes we measure with eddy covariance are assumed to be quasi-steady (or stationary) with horizontal homogeneity (Foken and Wichura, 1996). As Heraclitus once said, “all is flux, nothing is stationary” (Plato Cratylus, 402a). In nature, atmospheric flow is neither stationary, nor homogenous (Businger et al., 1971). Therefore, our flux measurement is impacted, and my research aims to target this impact by addressing the advection of heat and moisture that arise from spatiotemporal dynamics (e.g. wind and temperature/moisture gradient).

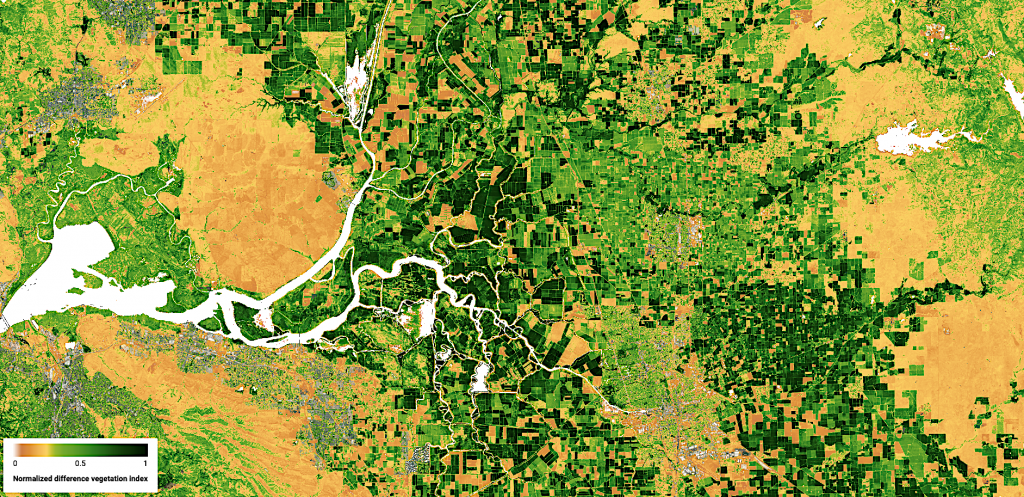
Fig. 1. A normalized difference vegetation index map over the Sacramento–San Joaquin River Delta showing the spatial mosaic pattern. The image is from Sentinel-2 overpass on Aug 22nd, 2021

In chess, the touch-move rule entails that a deliberately touched piece must move. Meanwhile in nature, you guessed it, things are constantly in motion. For example, in the Central Valley of California, irrigated agricultural fields (‘oasis’) are mosaicked with dry fields, forming a unique chess board pattern (Figure 1) that is susceptible to higher water loss via advection of sensible heat (Philip, 1959). Under heat advection, the sink of sensible heat flux pulls warmer air from the atmosphere and increases the evaporative demand. Subsequently, latent heat flux can oftentimes exceed the net available energy, impacting local evaporation rate (Baldocchi et al., 2016; Rosenberg and Verma, 1978; Tolk et al., 2006). It is also worth mentioning that advection is a collocated process, where regions with heat advection also experiencing moisture advection, and more research on this dynamic duo is underway. Commonly, for flux measurements, extensive fetch is intended upon deployment to minimize advection and seek homogeneity (Gash, 1986). With the patchiness embodying fallow, greening, full-canopy, and senescent lands (Figure 1), should the advection of heat and moisture be considered as a norm?

From my first year’s NASA FINESST (ROSES-2020) project, we revisited the enthalpy conservation budget (see Foken et al., 2012 – Chapter 1 Eq. 1.16) and extended measurements at US-Bi1 (https://ameriflux.lbl.gov/sites/siteinfo/US-Bi1). Particularly, secondary flux sensors were added at the main tower to measure flux divergence. Further upwind, another tower was deployed to measure flux divergence (at the tower) and lateral advection (between towers). On average, the vertical flux divergence was present but small, and the field was consistently under advective conditions of heat (Figure 2.). So, what caused this? Was it the advected heat or the entrained fluxes from an internal boundary layer? And what was the scale of this advection (i.e. intra-field, local, or regional)? To answer these questions, we may have to consult remote sensing.

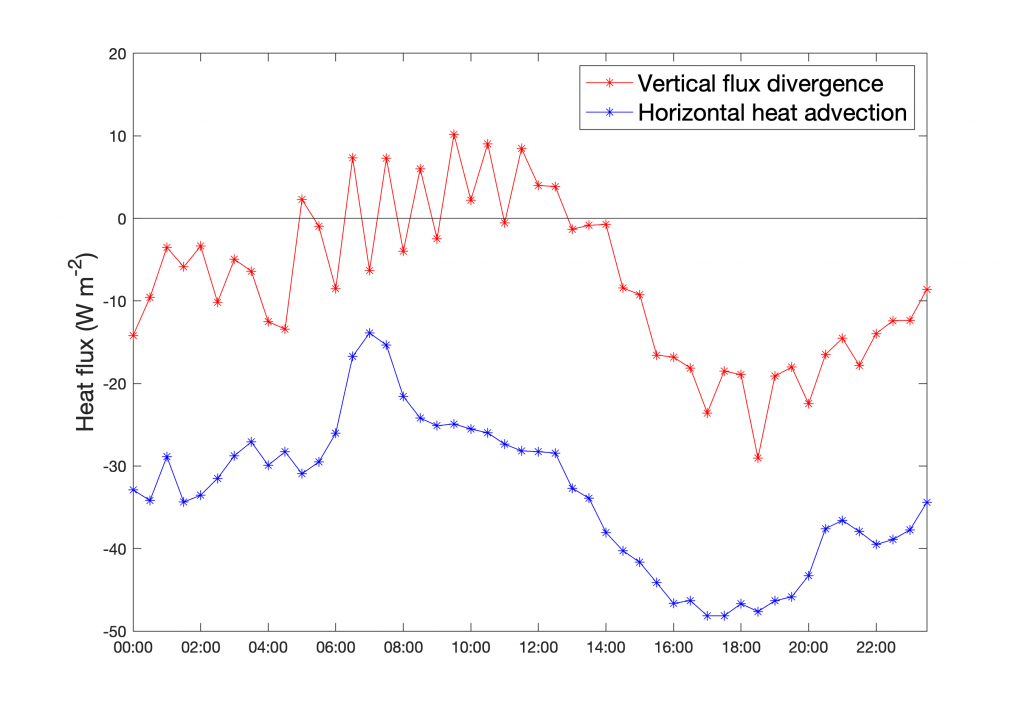
Fig. 2. An example of the diel conservation of vertical flux divergence and horizontal heat advection in the month of September 2021.

Advantageously, ECOSTRESS allows us to view the underlying problems from a zoomed-out view, where measurements can be linked to land-surface temperature observations. In Figure 3 (left panel), heat advection was high in the afternoon, resulting in the latent heat flux to exceed the net available energy. Specifically, during the ECOSTRESS overpass, though late in the afternoon, the measured heat advection was still around -55 W m^-2, indicating that the added heat energy did enhance the latent heat flux. Moreover, with the ECOSTRESS remotely sensed temperature gradient from US-Bi2 (~23°C) to the oasis-like US-Bi1 (~18°C), we can confirm that the latent heat enhancement was likely from sensible heat advection at a regional scale. This in-situ and remote sensing synergy is beneficial for improving current models as they often treat energy flux exchanges as individual columns, thus neglecting horizontal processes. Currently, we are working on resolving and modeling this horizontal movement of heat and moisture advection using flux measurement and satellite-based remote sensing data.

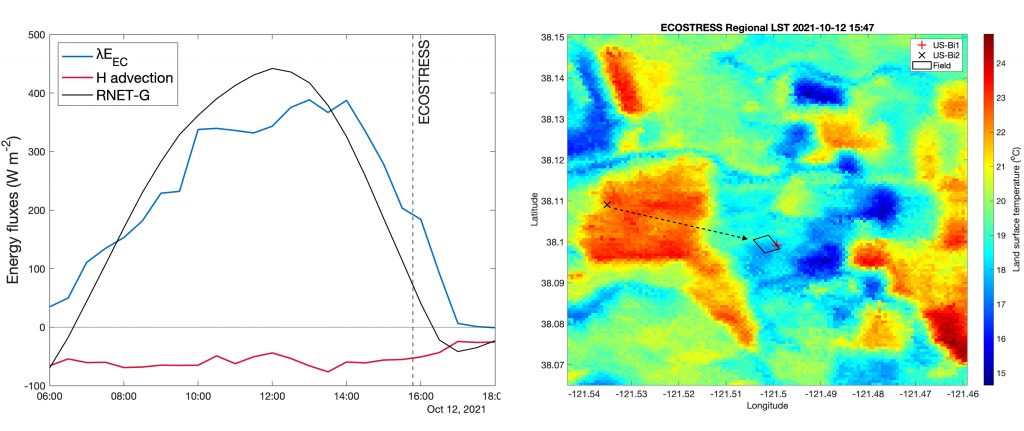
Fig. 3. (left) half-hourly energy fluxes of λE_EC (blue), sensible heat advection (red), and the net available energy (black); (right) ECOSTRESS land-surface temperature (LST) observation on 2021/10/12 at 15:47 local time. This scene includes US-Bi1 (red cross), US-Bi2 (black cross), and the predominant wind direction (dashed black line).

Building on last year pilot study, we recently set up a new advection campaign, including two additional towers to look at 1) horizontal advection and flux divergence of heat and moisture, and 2) vertical flux divergence of heat. This deployment was possible because of the wonderful team in the Biometeorology lab where I am pursing my PhD. Furthermore, through the AmeriFlux Management Project team loaner program (https://ameriflux.lbl.gov/tech/support-services/#loan), we added a LI-7500A sensor to this field campaign, allowing us to measure directly water fluxes at an additional location.

In this setup (Figure 4), the edgy tower measures fluxes from outside of the field. This essentially allows the establishment of the advection measurement with the edgy-to-bouncer transect. Similarly, another transect is established with the bouncer-to-main transect. Altogether, this allows us to investigate heat and moisture advection, and the evolution of surface energy fluxes along the transect.

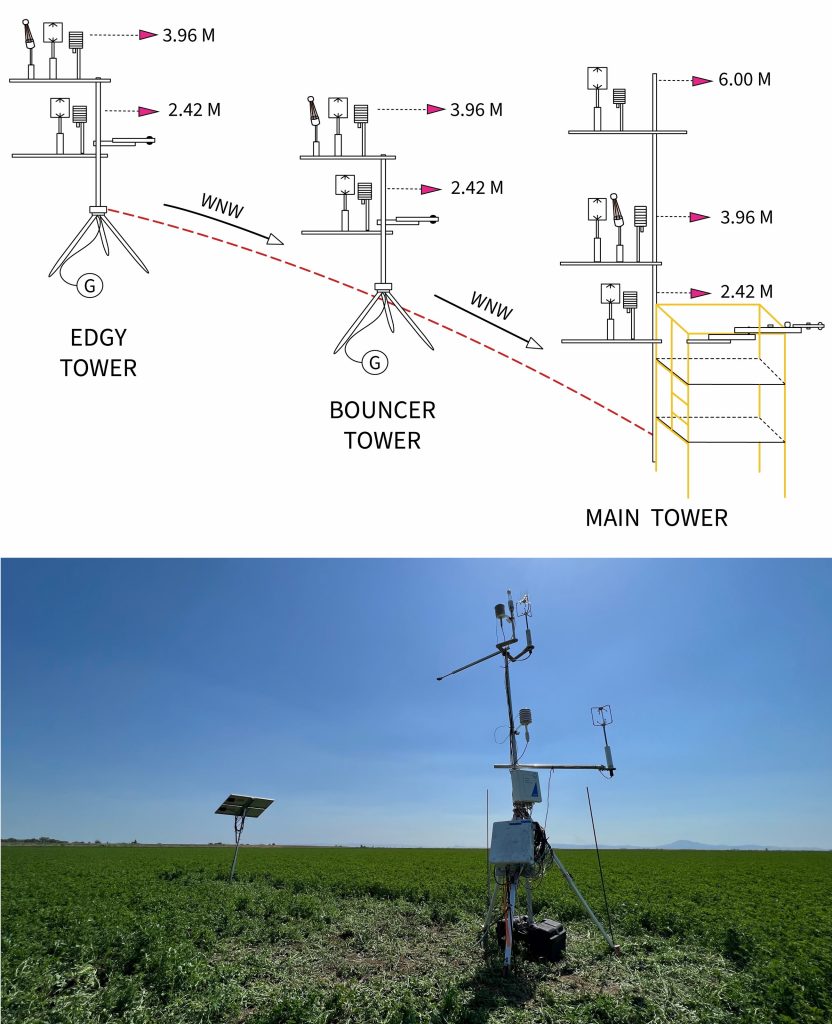
Fig. 4. (top) year 2 advection campaign design with edgy tower (by field edge), bouncer tower (in the field), and the main tower (further downwind); (bottom) the deployed and operating bouncer tower with some disturbed alfalfa near it.

In summary, the ubiquitous advection can induce uncertainties in field measurements, and field data are used to parameterize, validate, and calibrate remote sensing models (Alfieri et al., 2012). Thus, understanding the influence of advection on field measurements and quantifying limitations and uncertainties is a crucial first step in making remote sensing models more biophysically realistic. The outcomes from this research will help us to:

1. Model heat and moisture advection from space;
2. Better understand how co-located advection affect remote sensing models through advection of heat (DisALEXI) and moisture (PT-JPL);
3. Improve current evaporation models by incorporating advection;
4. Improve the understanding on the energy balance closure problem.

Fig. 5. (left) Joe and Daphne from the Biometeorology Lab setting up the 6 m sensor point on the main tower (US-Bi1);(right) me having some fun with photoshoots at the edgy tower after a long day of fieldwork.

Funding

This research was supported by NASA Future Investigators in NASA Earth and Space Science and Technology grant (80NSSC21K1624) and NASA ECOSTRESS grant (80NSSC20K0166).

References

Alfieri, Joseph et al. 2012. “On the Discrepancy between Eddy Covariance and Lysimetry-Based Surface Flux Measurements under Strongly Advective Conditions.” Publications from USDA-ARS / UNL Faculty.

Baldocchi, D. et al. 2016. “The Impact of Expanding Flooded Land Area on the Annual Evaporation of Rice.” Agricultural and Forest Meteorology 223: 181–93.

Businger, J. A., J. C. Wyngaard, Y. Izumi, and E. F. Bradley. 1971. “Flux-Profile Relationships in the Atmospheric Surface Layer.” Journal of the Atmospheric Sciences 28(2): 181–89.

Foken, Th., and B. Wichura. 1996. “Tools for Quality Assessment of Surface-Based Flux Measurements.” Agricultural and Forest Meteorology 78(1): 83–105.

Foken, Thomas. 2008. “The Energy Balance Closure Problem: An Overview.” Ecological Applications: A Publication of the Ecological Society of America 18(6): 1351–67.

Foken, Thomas, Marc Aubinet, and Ray Leuning. 2012. “The Eddy Covariance Method.” In Eddy Covariance: A Practical Guide to Measurement and Data Analysis, Springer Atmospheric Sciences, eds. Marc Aubinet, Timo Vesala, and Dario Papale. Dordrecht: Springer Netherlands, 1–19.

Gash, J. H. C. 1986. “A Note on Estimating the Effect of a Limited Fetch on Micrometeorological Evaporation Measurements.” Boundary-Layer Meteorology 35(4): 409–13.

Kljun, N., P. Calanca, M. W. Rotach, and H. P. Schmid. 2015. “A Simple Two-Dimensional Parameterisation for Flux Footprint Prediction (FFP).” Geosci. Model Dev. 8(11): 3695–3713.

Massman, W. J. 2000. “A Simple Method for Estimating Frequency Response Corrections for Eddy Covariance Systems.” Agricultural and Forest Meteorology. 104: 185-198. 104: 185–98.

Moore, C. J. 1986. “Frequency Response Corrections for Eddy Correlation Systems.” Boundary-Layer Meteorology 37(1): 17–35.

Philip, J. R. 1959. “THE THEORY OF LOCAL ADVECTION: I.” Journal of the Atmospheric Sciences 16(5): 535–47.

Rosenberg, Norman J., and Shashi B. Verma. 1978. “Extreme Evapotranspiration by Irrigated Alfalfa: A Consequence of the 1976 Midwestern Drought.” Journal of Applied Meteorology and Climatology 17(7): 934–41.

Tolk, Judy A., Steven R. Evett, and Terry A. Howell. 2006. “Advection Influences on Evapotranspiration of Alfalfa in a Semiarid Climate.” Agronomy Journal 98(6): 1646–54.

Twine, T. E. et al. 2000. “Correcting Eddy-Covariance Flux Underestimates over a Grassland.” Agricultural and Forest Meteorology 103(3): 279–300.

About

Tianxin “Carlos” Wang is a PhD Candidate in the  Department of Environmental Science, Policy, and Management at UC Berkeley